Pure Monopoly: Demand, Revenue And Costs, Price Determination, Profit Maximization And Loss Minimization
For a seller in a purely competitive market, the demand curve is completely elastic, and, therefore, horizontal in a price-quantity graph. A competitive seller can sell as much as he wants at the market price. However, the demand curve for all sellers in the market is downward sloping where demand quantity increases as prices decrease. For a pure monopolist, its supply is the entire market supply, and, thus, downward sloping. Since a monopoly is a price maker, it will determine what quantity of output will yield the greatest profits. But first, let us see how revenue is maximized. To simplify the following discussion, we assume that the monopolist will only charge a single price for its product and that it is not subject to government regulation.
Maximizing Revenue
In trying to maximize revenue, the monopolist has a dilemma: the monopolist can only sell more product if it lowers its prices, because it's demand curve slopes downward as demand curves generally do. Demand only increases with decreasing prices, but the marginal revenue gained by selling one additional unit will always be less than the price of that unit because the monopolist must sell all units at the lower price.
Except for the first unit, marginal revenue is always less than price. For instance, suppose a monopolist can sell 1 widget for $100, but it can sell 2 widgets for $90. Producing 1 widget, the monopolist has total revenue of $100; producing 2 widgets, and selling them for $90 apiece yields total revenue of $180. Therefore, the monopolist's marginal revenue is $80 (= $180 − $100), which is $10 less than the price necessary to sell 2 widgets. If it can only sell 3 widgets for $75, then its total revenue is $225, so its marginal revenue is only $45 (= $225 − $180). As the quantity produced increases, marginal revenue continually declines until it becomes zero, then negative.
Note that this is in contrast to the competitive market, where the competitive firm can sell all that it wants for the market price. Therefore, its marginal revenue = marginal price = market price. As the monopolist increases production, marginal revenue continually declines until it actually becomes negative. At this point, the monopolist is earning the maximum total revenue. More production after that point will cause total revenue to decline.
Total revenue can also be examined using demand elasticity. The monopolist will increase production as long as demand is inelastic, because increased quantities yields increased revenue. When demand becomes elastic, then increasing the quantity more decreases total revenue, so the monopolist will set its price where demand reaches unit elasticity, right before it becomes elastic. Or, if the market demand remains inelastic, then the monopolist will produce what the market demands.
For instance, a manufacturer that produces a successful lifesaving cancer drug will naturally produce as much of the drug as there are cancer victims who would benefit from the drug. To produce less, would reduce profits, since the manufacturer could easily charge a price that exceeds its ATC for the drug, because demand will not change much with the price (inelastic demand). On the other hand, to produce more of the drug than there are cancer victims would cause the price of the drug to fall, resulting in less revenue overall. Because the drug manufacturer has a patent for the drug, it has a monopoly. It also has a well-defined market of a specific size. Thus, it can maximize its own profits by charging the highest price that the victims and their insurance companies are willing or able to pay, knowing that the cancer victims will do whatever they can to pay the price. This is why several drug manufacturers greatly increased their prices recently, to take advantage of inelastic demand for their products.
Price Determination
Like the competitive firm, the monopolist will set its price when:
Marginal Revenue (MR) = Marginal Cost (MC)
Because as long as marginal revenue exceeds marginal cost, then producing an additional unit will increase profits. When marginal revenue equals marginal cost, then the monopolist looks to the demand curve to see what price that corresponds to. At that point, profit is maximized. If the monopolist increases production beyond MR = MC, then the marginal cost will be greater for each additional unit than marginal revenue, which will decrease profits, since costs continue to increase.
- ATC = Average Total Cost
- MR = Marginal Revenue
- MC = Marginal Cost
1 Productive Efficiency: MC = Minimum ATC
2 Allocative Efficiency: MC = Market Price
Monopoly Profit = (Price - ATC) × Quantity
Note that a monopoly does not have a supply curve because it sets the supply according to the demand. In most markets, the market price is determined by the intersection of the demand curve and supply curve. However, for a monopoly, the market price is not set by the intersection of the demand and supply curves, for the monopolist decides what the supply will be — the monopolist sets the price at which its profits are maximized, which will then determine what the supply will be.
To summarize, the monopolist finds the profit maximizing output by finding that quantity where marginal revenue = marginal cost, then projects that quantity on to the market demand curve to determine what market price corresponds to that quantity. The monopolist's economic profit is then equal to the average revenue minus the ATC (ATC) multiplied by the number of units sold:
| Monopoly Profit | = (Price - ATC) × Quantity |
| = (Average Revenue × Quantity) - (ATC × Quantity) = Total Revenue - Total Cost |
This analysis refutes 2 common misconceptions about monopoly pricing: that the monopolist charges the highest price possible and that it seeks a maximum per unit profit. Obviously, the above analysis demonstrates that monopolies do not charge the highest prices because it doesn't yield the maximum profit. After all, the highest price could be charged only if the monopolist produced 1 unit of output. Obviously, it could never cover its fixed costs by producing only 1 unit of output, so it will not charge the highest price possible.
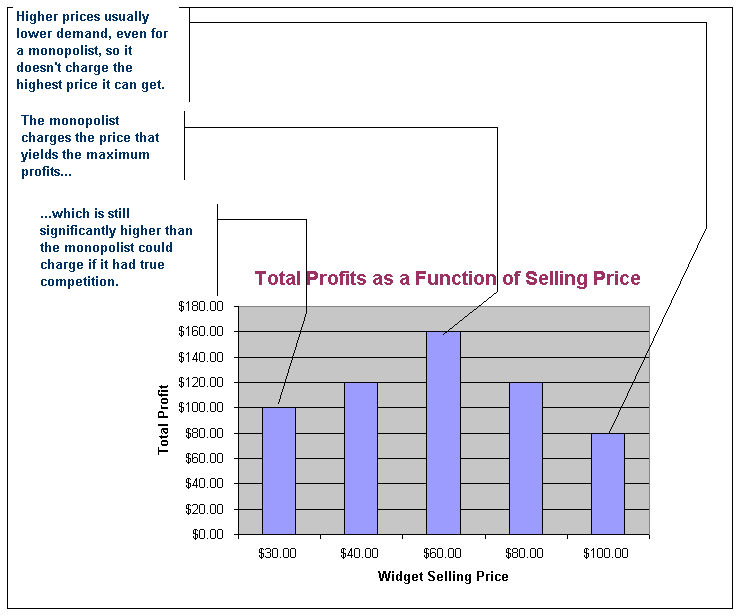
Since profit maximization is the goal, profits can always be increased as long as marginal revenue exceeds marginal cost. Hence, the monopolist has no interest in maximizing per unit profit, since this does not yield the greatest profit.
How a Monopolist Minimizes Losses
It is possible that a monopolist can actually lose money if ATC exceeds the price that people are willing to pay for any quantity of output. Losses can be caused by a change in consumer tastes or by changes in the cost of inputs. However, if the monopolist cannot make a profit, then it will shutdown the firm so it can put the resources to better uses. A monopolist will only produce in the short run to minimize losses if it perceives that market conditions will change or that it will be able to earn a profit in the future.
In this case, the monopolist will still produce the quantity where marginal revenue equals marginal cost because that quantity corresponds to the market price that will minimize its losses. Its losses will then be equal to:
Monopoly Loss = (ATC − Price) × Quantity