Bond Yields
The investment return of a bond is the difference between what an investor pays for a bond and what is ultimately received over the term of the bond. The bond yield is the annualized return of the bond. Thus, bond yield will depend on the purchase price of the bond, its stated interest rate, usually called the coupon rate — which equals the annual payments by the issuer to the bondholder divided by the par value of the bond — + the amount paid at maturity, which is the face value, often called the par value. Because the coupon rate and par value are stipulated in the bond indenture, the price of the bond will vary inversely to prevailing interest rates. If interest rates rise, then the price of the bond must decrease to remain competitive with other investments, and vice versa. Taxes may also reduce the actual return received by an investor, so high-income investors will be more interested in the taxable equivalent yield, the after-tax yield, to more easily compare taxable bonds and tax-exempt bonds.
The price, and therefore the yield, of the bond will also depend on the creditworthiness of the issuer, which indicates the risk of the investment. The higher the credit rating of the issuer, the lower the coupon rate the issuer must offer to sell its bonds. Changes to the credit rating of the issuer will also affect the market price of its bonds.
But interest rates are usually the major factor affecting bond prices and yields. The prevailing interest rate — the cost of money — is determined by the supply and demand of money. As for virtually everything else, supply and demand determine price, so for bonds, the greater the supply and the lower the demand, the lower the price of the bond and, correspondingly, the higher its yield, and vice versa.
Most bonds pay interest semi-annually until maturity, when the bondholder receives the par value, or the bond principal, of the bond back. Zero coupon bonds pay no interest, but are sold at a discount to par value, so the interest, which is the difference between par value and the discounted issue price, is paid when the bond matures. Nonetheless, the yield of the zero coupon bond is the annualized return, which allows it to be compared to coupon bonds.
To more easily compare bond yields, there are several different types of yields that can be calculated, including the nominal yield, current yield, yield to maturity, and the taxable equivalent yield.
Nominal Yield, Coupon Rate
Nominal yield, or the coupon rate, is the stated interest rate of the bond. This yield percentage is the percentage of par value —$5,000 for municipal bonds, and $1,000 for most other bonds — that is usually paid semiannually. Thus, a bond with a $1,000 par value that pays 5% interest pays $50 dollars per year in 2 semi-annual payments of $25. The return of a bond is the return/investment, or in the example just cited, $50/$1,000 = 5%.
| Nominal Yield | = | Annual Interest Payment Par Value |
Current Yield
Because bonds trade in the secondary market, they may sell for less or more than par value, which will yield an interest rate that is different from the nominal yield, called the current yield, or current return. Since bond prices move oppositely of interest rates, bond prices decrease when interest rates increase, and vice versa. To see why, consider this simple example. You buy a bond when it is issued for $1,000 that pays 8% interest. Suppose you want to sell the bond, but since you bought it, the interest rate has risen to 10%. You must sell your bond for less than what you paid, because why will somebody pay you $1,000 for a bond that pays 8% when they can buy a similar bond with an equal credit rating and get 10%. So to sell your bond, you must sell it so that the $80 annual interest payment will be 10% of the selling price — in this case, $800, $200 less than what you paid for it. (Actually, the price probably wouldn't go this low, because the yield-to-maturity is greater in such a case, since if the bondholder keeps the bond until maturity, he will receive a price appreciation which is the difference between the bond's par value of $1,000 and what he paid for it.) Bonds selling for less than par value are said to be selling at a discount. If the market interest rate of a new bond issue is lower than what you are getting, then you will be able to sell your bond for more than par value — you will be selling your bond at a premium. Note, however, that the bond price is based on the clean price, meaning that any accrued interest is excluded, since that will be paid to the bond owner on the next interest payment.
| Current Yield | = | Annual Interest Payment Current Market Price of Bond |
| Current Yield Example | ||
|---|---|---|
| $60 Annual Interest Payment $800 for Bond | = | 7.5% Current Yield |
Note that if the bond's market price = its par value, then:
Current Yield = Nominal Yield
Taxable Equivalent Yield (TEY) for Munis and Treasuries
The interest from municipal bonds is not taxed by the federal government, and U.S. Treasury bonds, notes, and T-Bills do not incur state or local taxes. Additionally, municipal interest is also exempt from the new 3.8% Net Investment Income Tax (Medicare surtax) assessed on investment income. Hence, these bonds can pay a lower interest rate than a corporation with a comparable credit rating. To compare municipal bonds or Treasuries with taxable bonds, the yield is converted to a taxable equivalent yield (TEY), sometimes called equivalent taxable yield. The taxable equivalent yield is the yield that a taxable bond must pay to be equivalent to the tax-free bond.
| Taxable Equivalent Yield (TEY) | = | Muni Yield 100% − Your Federal Tax Bracket % − 3.8% Net Investment Income Tax |
| Taxable Equivalent Yield Example | ||||
|---|---|---|---|---|
| TEY | = | 4% Muni Yield 100% − 37% Federal Tax Bracket − 3.8% NIIT | = | 6.76% |
We can call this the federal taxable equivalent yield, but note that if you live in the municipality of the bond issuer, then the bond may be free of state and local taxes as well. To take in consideration all taxes saved, the above formula can be extended for any tax situation by simply adding up the percentages to arrive at a composite tax bracket and use that in the above equation to get the tax-free yield.
| Taxable Equivalent Yield Example for Municipal Bond Exempt of All Taxes | ||||
|---|---|---|---|---|
| TEY | = | 6.1% Muni Yield 100% − 37% federal tax − 3.8% NIIT − 10% state tax − 1% local tax | = | 12.66% |
To look at it from a different angle, suppose a bond pays 12.66%, as in the above example. That's $126.60 per year for a par value of $1,000. If you pay 37% of your income in federal taxes, 3.8% in NIIT, 10% in state taxes, and 1% in local taxes, and the bond is taxable, then the federal tax = $46.84, the NIIT = $4.81, the state tax = $12.66, and the local tax = $1.27 — a net of $61.02. A tax-free municipal bond yielding 6.1% would net the same amount. U.S. Treasuries do not incur state or local taxes, but federal taxes have to be paid on the interest, so the taxable equivalent yield for Treasuries is calculated using the same formula, but only the state and local tax rate is deducted from 100%.
| Taxable Equivalent Yield (TEY) | = | Treasury Yield 100% − State Tax Rate % − Local Tax Rate % |
| Taxable Equivalent Yield Example for U.S. Treasuries | ||||
|---|---|---|---|---|
| TEY | = | 4% Treasury Yield 100% − 10% state tax − 1% local tax | = | 4.5% |
Thus, a corporate bond taxable by the federal, state and local government must pay 4.5% to net the same amount that a U.S. Treasury paying 4% would net. Note, also, that U.S. Treasuries are considered the safest investment, so the corporate bond must pay a little more — even if it had the highest credit rating — than the Treasury, to compensate the investor for the small additional risk. The lower the credit rating of the corporate bond, the greater the interest the corporate bond must pay to entice investors away from safe, risk-free Treasuries.
Yield to Maturity or True Yield
If an investor buys a bond for a price different from par value, then not only will the current yield differ from the nominal yield, but there will be a gain or loss when the bond matures and the bondholder receives the par value of the bond. Like the calculation for current yield, yield to maturity and other yields based on the purchase price of the bond in the secondary market is based on the clean bond price, excluding accrued interest. An investor holding the bond until maturity will lose money if the bond was bought at a premium or earn money if bought at a discount. The yield-to-maturity (YTM) (aka true yield, effective yield) of a bond held to maturity accounts for the gain or loss that occurs when the par value is repaid, so it is a better measure of the investment return.
When a bond is bought at a discount, yield to maturity will always exceed the current yield because there will be a gain when the bond matures, when the bondholder receives par value back, thus raising the true yield; when a bond is bought at a premium, the yield to maturity will always be less than the current yield because there will be a loss when par value is received, which lowers the true yield.
| When | Bond Yield Relationships |
|---|---|
| Market Price < Par Value (discount). | Yield to Maturity > Current Yield > Nominal Yield |
| Market Price = Par Value | Nominal Yield = Current Yield = Yield to Maturity |
| Market Price > Par Value (premium). | Nominal Yield > Current Yield > Yield to Maturity |
Yield to Call
Callable bonds also have a yield to call (YTC), calculated like the yield to maturity, but the call date is substituted for the maturity date and the call price or call premium is substituted for par value. When a bond is bought at a premium, the yield to call is always the lowest yield of the bond. If the bond is purchased at a discount, then the yield to call will exceed the yield to maturity since the gain from redemption will be received sooner than maturity.
Yield to Sinker
Some bonds are redeemed periodically by a sinking fund — also called a mandatory redemption fund — that the issuer establishes to retire debt periodically at sinking fund dates specified in the redemption schedule of the bond contract for specified sinking fund prices, which are often just par value. Such bonds are usually selected at random for redemption on such dates, so yield to sinker is calculated as if the bond will be retired at the next sinking fund date. If the bond is retired, then the bondholder simply receives the sinking fund price, and so the yield to sinker is calculated like the yield to maturity, substituting the sinking fund date for the maturity date, and, if different, substituting the sinking fund price for the par value.
Note, however, that yield to call and yield to sinker may not be pertinent if interest rates have risen since the bonds were first issued, because these bonds will be selling for less than par value in the secondary market, and it would save the issuer money to simply buy back the bonds in the secondary market, which helps to support bond prices for bondholders who want to sell.
Yield to Average Life
The yield to average life calculates the yield using the average life of a sinking bond issue. So for a 20-year bond with an indenture that specifies that 10% of an issue must be retired each year from the 10th year to the 20th year of the bond's term, the average life would be 15 years.
The yield to average life is also used for asset-backed securities, especially mortgage-backed securities, because their lifetime depends on prepayment speeds of the underlying asset pool.
Yield to Put Option
Some bonds have a put option, which allows the bondholder to receive the principal of the bond from the issuer when the bondholder exercises the put. This yield to put would be calculated like the yield to maturity, except that the date that the put is exercised is substituted for the maturity date, because the bondholder receives the par value on the exercise date just as if the bond matured.
Yield to Worst
Finally, there is the yield to worst, which is the lower of the yield to call or the yield to maturity . This yield is most often listed along with the yield to maturity in the listings of bonds sold in the secondary market provided by brokers because it is the yield that most investors will want to know.
The Formula Relating a Bond's Price to its Yield to Maturity, Yield to Call, or Yield to Put
The formula below shows the relationship between the bond's price in the secondary market (excluding accrued interest) and its yield to maturity, or other yields, depending on the maturity date chosen. In this equation, which assumes a single annual coupon payment, YTM would be the bond's yield to maturity, but this is difficult to solve, so bond traders usually read the yield to maturity from a table that can be generated from this equation, or they use a special calculator or software, such as Excel as shown further below. Yield to call is determined in the same way, but n would equal the number of years until the call date instead of the maturity date, and P would be the call price. Similarly, the yield to put, or any of the other yields, is calculated by substituting the appropriate date when the principal will be received for the maturity date.
| Bond Price | = | C1 (1+YTM)1 | + ... + | Cn (1+YTM)n | + | P (1+YTM)n |
or, expressed in summation, or sigma, notation:
| B = | n ∑ k=1 | Ck (1+YTM)k | + | P (1+YTM)n |
Note that if the bond pays a semiannual coupon, as most US bonds do, then the following formula applies:
| Bond Price | = | C1 (1+YTM/2)1 | + ... + | Cn (1+YTM/2)2n | + | P (1+YTM/2)2n |
This equation shows that the bond price = the present value of all bond payments with the interest rate equal to the yield to maturity. Although it is difficult to solve for the yield using the above equation, it can be approximated by this formula:
| Approximate Yield-to-Maturity Yield Percentage | = | AIP + (PV − CBP)/Years (PV+ CBP)/2 |
- AIP = Annual Interest Payment
- PV = Par Value
- CBP = Current Bond Price
- Years = Number of Years until Maturity
| Yield-to-Maturity Example | |
|---|---|
| $60 + ($1,000 - $800)/3 ($1,000 + $800)/2 | ≈ 14% |
| |
Note that if a premium was paid for the bond, then the term (Par Value - Current Bond Price)/Number of Years until Maturity would be subtracted from the annual interest payment rather than added to it, since it would be a negative number. A good way to remember this formula is that it is simply taking the difference between the par value and the current bond price and dividing it by the remaining term of the bond. This is the profit or loss per year, which is then added to or subtracted from the annual interest payment. The resulting sum, in turn, is divided by the average of the par value and the current bond price. Once the bond is bought, then the yield to maturity is fixed, so the current bond price is replaced with the purchase price in the above formula.
A simplification of the YTM formula can be made if the bond has no coupon payments, since all the terms involving coupon payments become zero, and the yield to maturity reduces to the present value of the principal payment (Formula #1 below):
| 1. | Discounted Bond Price | = | Principal Payment (1+YTM)n |
| 2. | Present Value | = | Future Value (1+YTM)n |
Note that equations #1 and #2 above are the same, since the discounted bond price is the present value of the investment and the principal payment is the future value, so we can find a simple way to calculate YTM by using a basic formula for the present value and future value of money. To find the yield to maturity, we transpose the equation for the future value of money to equal the yield to maturity. The equation for future value, which can be obtained by multiplying both sides of Equation #2 by (1 + YTM)n, is:
Present Value * (1 + YTM)n = Future Value
Divide both sides by the Present Value:
(1 + YTM)n = Future Payment/Present Value
Take the nth root of both sides:
1 + YTM = (Future Payment/Present Value)1/n
Then subtract 1 from both sides, to arrive at YTM, the yield to maturity for the discount:
| r= | ( | FV PV | ) | 1/n | − 1 |
| r = YTM per time period n = number of time periods FV = Future Value PV = Present Value | |||||
or
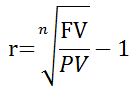
| YTM Example for a Zero Coupon Bond | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| If
Then
To check our result, we plug the YTM into the YTM formula:
|
Note that the above example is compounded annually. To find the YTM compounded biannually, simply set n=20 and multiply the resulting YTM for a 6-month period by 2:
YTM = (100/60)1/20 - 1 = 0.025870255 × 2 = 0.051741 ≈ 5.17%
Note that the YTM is slightly lower because it is compounded twice a year instead of once a year, so it must be lower to yield the same payment amount of $40 at maturity. To check the result:
Discounted Bond Price = 100/1.0258720 = 100/1.666666667 ≈ $60
YTM can also be readily solved by using Microsoft Excel, as shown below.
| YTM = Yield(settlement, maturity, rate, price, redemption, frequency, basis) All dates are expressed either as quotes or as cell references (e.g., "1/5/2013", A1).
Note that yield to call (YTC) and yield to put (YTP) can also be calculated using this formula. To calculate the yield to call:
To calculate yield to put:
Yield to Worst, Yield to Sinker, and Yield to Average Life can be calculated by substituting |
| Yield to Maturity (YTM) Example |
|---|
| If
Then
|
Using the YTM approximation formula for the above example yields nearly the same result:
| Yield-to-Maturity Example Using Approximation Formula | |||
|---|---|---|---|
| $50 + ($1,000 - $925.60)/10 ($1000 + $925.60)/2 | = | $57.44 $962.80 | |
| = | 0.059659327 | ≈ 6% | |
Horizon Yield (aka Realized Compound Yield)
The horizon yield (aka realized compound yield) is the yield obtained by reinvesting all coupon payments for additional interest income. It will also depend on the bond price if it is sold before maturity. This yield ultimately depends on how interest rates change over the holding period of the bond. Although future interest rates and bond prices cannot be predicted with certainty, horizon analysis is often used to forecast interest rates and bond prices over a specific time period to yield an expectation of the realized compound yield.
Holding-Period Return
Yield to maturity is the average yield over the term of the bond. If a bond is sold before maturity, then its actual yield will differ from the yield to maturity. If interest rates rise during the holding period, then the bond's sale price will be less than the purchase price, decreasing the yield, and if interest rates, decrease, then the bond's sale price will be greater. The holding-period return is the actual yield earned during the holding period. It can be calculated using the same formula for yield to maturity, but the sale price would be substituted for the par value, and the term would equal the actual holding period. Note that, unlike yield to maturity, the holding-period return cannot be known ahead of time because the sale price of the bond cannot be known before the sale, although it could be estimated.
Bond Equivalent Yield (BEY)
Money market instruments are short-term discount instruments with maturities of less than a year, so the interest is paid at maturity. Because short-term instruments are issued at a discount, their yield is called a discount yield, which is often annualized as the bond equivalent yield (BEY) (aka investment rate yield, equivalent coupon yield), which simplifies the comparison of yields with other financial returns:
BEY = Interest Rate per Term × Number of Terms per Year
| Interest Rate Per Term | Number of Terms per Year | ||
| BEY = | Face Value - Price Paid Price Paid | × | Actual Number of Days in Year Days Till Maturity |
Although the BEY is not compounded, but is simply the discount yield annualized, it can be converted directly to any compounded rate of interest by using the formula for the present and future value of a dollar. (See Calculating the Interest Rate of a Discounted Financial Instrument for more info.)
To find a compounded rate, add 1 to the discount yield and raise the result to a power equal to the number of terms in the year, then subtract the result from 1:
Compounded BEY Rate = (1 + Discount Yield) n − 1
- n = Number of Terms in the Year
So if the discount yield is 1% for 90 days, then, using a banker's year of 360 days, the compounded BEY rate is calculated thus:
- Number of Terms in Year = 360/90 = 4
- Compounded BEY Rate = (1 + .01)4 − 1 = 1.014 − 1 = 1.0406 − 1 =.0406 = 4.06%
Example: Calculating the Bond Equivalent Yield of a T-Bill
If you buy a 4-week T-bill with a face value of $1,000 for $997, what is the bond equivalent yield, assuming it is not a leap year?
($1,000-$997)/$997 × 365/28 ≈ 3.92% (rounded)
Example: Formula for Finding the Annualized Effective Compounded Rate of Interest for a Discounted Note
To find the compounded rate of interest for a discounted money market instrument:
- Divide the par value by the discounted price.
- Raise the result by the number of terms in 1 year, then subtract 1.
If you bought a 4-week T-bill for $997 and receive $1,000 4 weeks later, what is the effective annual compounded interest rate earned?
Solution:
- $1,000/$997 = 1.003009 (rounded)
Since there are 13 4-week periods in a year, $1 compounded 13 times would equal:
- (1.0035)13 - 1 = 1.040 - 1 = 4.0% (rounded)
(See how the future value of a dollar is calculated to understand the reasoning better.)
This formula can calculate the yields of any financial instrument sold at a discount.
Perpetuities (aka Perpetual Bonds, Annuity Bonds, Consols)
Perpetuities are bonds that are not redeemable and pay only interest, but pay it indefinitely — hence the name. They do not mature and, thus, the principal is never repaid. They were first issued by the British government in the 1850's, and were called consols, and some perpetuities were issued by the U.S. Treasury, but perpetuities are very rare today.
The price of a perpetuity = the present value of all future payments. While this forms an infinite series, it does have a finite limit, because successive terms become smaller and smaller, and that limit is the following:
Price of Perpetuity = Annual Coupon Payment / Nominal Interest Rate
Consequently, the yield of a perpetuity is calculated as the current yield:
Yield of Perpetuity = Current Yield = Annual Coupon Payment / Perpetuity Price
Note that because a perpetuity is not redeemable and pays no principal, a perpetuity has no yield to maturity, since it never matures.
Example: Calculating the Yield of a Perpetuity
If
- Perpetuity annual coupon payment = $1
- Perpetuity price = $20
Then
- Perpetuity Yield = 1 / 20 = 5/100 = 5%.
Risk Structure of Interest Rates
U.S. Treasuries are generally considered free of default risk, and therefore generally have the lowest yield. All other bonds have some risk of default — some more than others. To compensate investors for the greater risk, these bonds pay a higher yield. This difference in yield is known as the risk premium (aka default premium), and how the risk premium varies across different bonds and different maturities is known as the risk structure of interest rates. The greater the risk of default, the greater the risk premium.
During a recession, investors become more concerned that the risk of default will increase, since recessions can cause financial difficulties for companies. So many investors move their investments to safer bonds — a flight to quality. This increases the difference in yield between corporate bonds and riskless government bonds. As a result of the lower demand, the default premium increases to compensate investors for the greater risk.