Moving Averages
The highest trading profits are made in strongly trending markets, and the best way to detect trends and changes in trends is by using moving averages. Moving averages are average prices of a security or index over a specific time interval that is continually updated. Because prices are averaged, the daily fluctuations are dampened into a smoother line that better represents the current trend. The strength of the trend is indicated by the slope of the moving average, especially longer-term moving averages. Moving averages are also used in other technical indicators, such as Bollinger Bands, envelopes, and directional movement indicators.
Simple Moving Averages (SMA)
A simple moving average (SMA) is simply the average of prices of a security or index over a specific time span, such as 5, 10, 20, or 50 days. They are called moving averages because they are calculated for each trading day for the previous period, so at the end of a trading day, the last day is added, while the earliest day of the previous average is dropped. Most moving averages are based on closing prices, but they can be based on opening, high, low, or mean prices. Whichever price is chosen must be used consistently to give the best indication of trend.
Example: to calculate a 10-day simple moving average, which can be denoted as SMA(10), based on closing prices, the closing prices of the last 10 days are added, then divided by 10. After the next trading day, the earliest day of the previous average is replaced by the latest day.
| SMA(days) | = | days ∑ k=1 | Price on Day k Number of Days |
Example: Calculating a Simple Moving Average
If the last 3 closing prices of a stock are $9, $11, and $12, what is its 3-day simple moving average?
SMA(3)
- = (9 + 11 + 12) / 3
- = 32 / 3
- = 10.67
Since a simple moving average is only an average where the last value is added and the first value is dropped for each day, a simple moving average can also be calculated using a spreadsheet's AVERAGE function. Thus, with Microsoft Excel, this moving average can be calculated thus:
SMA(3) = AVERAGE(9,11,12) = 10.67
The input variables to the AVERAGE function can be references to cells with imported stock prices, which makes their calculation even easier.
Because moving averages are based on data in a preceding period, they are lagging indicators. They can only indicate a trend that is already in place. Moving averages based on shorter time spans more closely reflect the underlying current trend, but they are also more sensitive to the volatility of the markets, which can spawn many false signals.
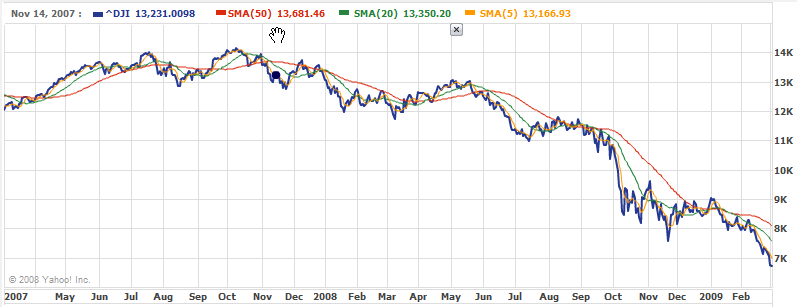
To minimize false signals, especially in a whipsaw market that trades within a narrow range, multiple moving averages of different time spans are used together. Traders often use crossovers, where the graph of the shorter moving average crosses over a longer moving average, as a good indication of a new trend. Traders often use the crossovers as a buy or sell signal and as a good price to set trailing stops. So if the shorter moving average crosses above the longer-term average, then this indicates a beginning of an uptrend, while a downward cross may indicate the beginning of a downtrend. However, even crossovers may give false signals, particularly in whipsaw markets, so moving averages are often used with other technical indicators as a confirmation of the trend change.
Exponential Moving Averages (EMA)
The problem with simple moving averages is that the earliest day of the time period has the same weight in the average as the most recent day. If the earliest day was volatile, but the market recently calmed, then the volatile day will have a large influence on the average — called a drop-off effect — which would not best represent the current market. To correct this anomaly, exponential moving averages (EMA) are used, where greater weight is given to more recent prices. This greater weight causes the EMA to usually follow the underlying prices more closely than the SMA of the same duration.
Moving averages can be calculated in many different ways, but the traditional method of calculating the EMA is to add an additional day to the simple moving average, then give greater weight to the last day. So for a 10-day moving average, the EMA uses 11 days, with the last day given a weight of 2/11 of the average, which equals 18.18%. The formula to calculate the weight of the last day is:
Weight current = 2 / (Number of Days in Moving Average + 1)
Since the sum of all the weights must equal 100%, the weights of the preceding 10 days must equal:
WeightMA = 100% − Weightcurrent
For this example, the weight of the preceding 10 days is 100% - 18.18% = 81.82%.
Hence, the formula for calculating the exponential moving average is:
EMA
- = Last Day Weight × Last Day Price
- + ( Weight of Previous Exponential Moving Average
- × Previous Exponential Moving Average )
So if JXYZ stock had a 10-day moving average of 25 yesterday, and the stock closed at 26 today, then:
EMAXYZ
- = 26 × 18.18% + 25 × 81.82%
- = 4.73 + 20.46
- = 25.18
For each trading day, the previous EMA is used to calculate the new EMA, so if on day 12, JXYZ stock closed at 27, then the new EMA equals:
EMA JXYZ
- = 27 × 18.18% + 25.18 × 81.82%
- = 4.91 + 20.60
- = 25.51
The exponential moving average has many variations, many based on calculations of the EMA on the volatility of the market.
Trading Strategies Using Moving Averages and Crossovers
Moving averages can easily be calculated using a spreadsheet or the software of a trading platform. Most major websites that provide stock prices, such as Yahoo, Google, and Bloomberg, also provide free charting tools that include moving averages. Most of these tools also allow multiple moving averages to be plotted in the same graph — even SMAs and EMAs can be combined in the same graph.
As stated earlier, moving averages can be calculated in many ways, and, likewise, can be used in many ways. No persuasive evidence indicates that any method is better than any other, especially since infinite combinations of moving averages and other technical indicators are possible.
The best use of moving averages is in determining trends. The greater the slope of the moving average, the greater the strength of the trend. Generally, traders will choose a time period that is suitable to their investment time frame. So a long-term trader will use a 200-day average or longer, while a swing trader will use much shorter time frames.
Crossovers of 1 or more moving averages over a longer-term moving average usually signify a change in trend and are also used as trading signals or to set trailing stops.
Another use of moving averages is to detect and profit from extreme prices. Prices that suddenly stray far from the average often revert to the average in the short term if there is no significant news causing the price deviation, so short-term traders can profit from these deviations.
Moving Average Convergence-Divergence (MACD) Indicator
A moving average provides no trading signal and a crossover of 2 or more moving averages may come too late to profit from a change in trend. Some traders, hoping to act early to take advantage of anticipated signals, look at the converging lines to see if they are likely to cross over or if the lines are diverging, reducing the likelihood of a crossover. But this is trading by intuition. Convergence and divergence can be quantified to create a signal.
Convergence is the coming together of 2 or more indicators. With moving averages, it could be the sign of an impending change in trend.
Divergence is the moving apart of 2 or more indicators. With moving averages, this indicates that the trend is likely to continue. However, if the divergence is too sharp, then prices may be reaching an extreme level and are likely to pull back soon.
A simple way to calculate convergence and divergence is to subtract the long-term moving average from the short-term average, then plot it as a line graph. If the line moves toward zero, then the moving averages are converging and when they cross over, the difference is zero. If, however, the difference is growing larger, then the 2 moving averages are diverging.
Gerald Appel figured that by plotting the difference between the 2 moving averages against a moving average of the difference, specific trading signals can be produced, called the moving average convergence-divergence indicator (aka MACD indicator).
Though most any moving average can be used to plot either the moving averages of the security, or the moving average of the MACD indicator, Appel used the 12- and 26-day moving average for the security, and the 9-day moving average for the MACD indicator. This is shown in the graph of Google (GOOG) below. Note how the MACD indicator usually crosses over well before the 2 moving averages of the security, and successfully indicates the change in trend at several places. The MACD is still a lagging indicator, but it lags much less than the moving averages of the security. Remember, like moving averages, the MACD indicator sometimes gives false signals.