Bond Formulas
This page lists the formulas used in calculations involving money, credit, and bonds. If you want to learn about these topics in detail, illustrated with detailed examples, please read the referring page.
Present Values and Future Values of Money
From The Present Value and Future Value of Money.
| FV | = | PV × (1 + r)n |
| PV | = | FV (1 + r)n |
- PV = Present Value
- FV = Future Value
- r = interest rate per time period
- n = number of time periods
- i = Interest Rate of Discount per time period
| i | = | ( | FV PV | ) | 1/n | − 1 |
or
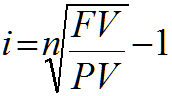
From The Present Value and Future Value of an Annuity.
| FVOA | = | A | × | (1 + r)n − 1 r |
| FVAD | = | A | × | (1 + r)n − 1 r | + | A(1+r)n | − | A |
| PVA | = | n ∑ k=1 | A (1+i)k |
- PVA = Present Value of Annuity Amount
- A = annuity payment
- i = interest rate per time period
- n = number of time periods
| PVA | = | A * | 1− | 1 (1 + i)n |
i | ||||
| A | = | PV 1−(1+i)−n i | = | PV * | i 1−(1+i)−n |
- PV = present value, or the amount of the loan.
Bond Yields
From Bond Yields.
| Nominal Yield | = | Annual Interest Payment Par Value |
| Current Yield | = | Annual Interest Payment Market Price of Bond |
| Taxable Equivalent Yield | = | Muni Yield 100% − Your Federal Tax Bracket % |
| Approximate Yield-to-Maturity % | = | [Annual Interest + (Par Value − Bond Price)/Years till Maturity] (Par Value + Bond Price)/2 |
A more accurate calculation of yield to maturity or yield to call or yield to put:
| Bond Price | = | C1 (1+YTM)1 | + | C2 (1+YTM)2 | + ... + | Cn (1+YTM)n | + | P (1+YTM)n |
- C = coupon payment per period
- P = par value of bond or call premium
- n = number of years until maturity or until call or until put is exercised
- YTM = yield to maturity, yield to call, or yield to put per pay period, depending on which values of
n and P are chosen.
or, expressed in summation, or sigma, notation:
| B | = | n ∑ k=1 | Ik (1+Y)k | + | P (1+Y)n |
| i = | (Future Value/Present Value)1/n − 1 | |
- i = interest rate per compounding period
- n = number of compounding periods
- FV = Future Value
- PV = Present Value
or
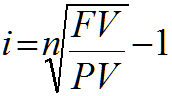
| Interest Rate Per Term | Number of Terms per Year | ||
| BEY = | Face Value − Price Paid Price Paid | × | Actual Number of Days in Year Days Till Maturity |
From Bond Pricing, Illustrated with Examples
| Accrued Interest | = | Interest Payment | × | Number of Days Since Last Payment Number of days between payments |
From Volatility Of Bond Prices In The Secondary Market; Duration and Convexity
| T ∑ t=1 | t × Ct (1 + y)t | |
| D = | ||
| T ∑ t=1 | Ct (1 + y)t | |
- D = Macaulay duration
- t = time until payment in years
- T = total number of payments
- Ct = cash flow at time t
- y = bond yield until maturity
Note that the denominator = the sum of all cash flows discounted by the yield to maturity, which = the bond's price.
Duration and Convexity
From Duration and Convexity, with Illustrations and Formulas
Bond Value = Present Value of Coupon Payments + Present Value of Par Value
| Duration | = | P- − P+ 2 × P0(Δy) |
- P0 = Bond price.
- P- = Bond price when interest rate is incremented.
- P+ = Bond price when interest rate is decremented.
- Δy = change in interest rate in decimal form.
| Macaulay Duration | = | T ∑ t=1 | t | × | wt |
- T = number of cash flow periods.
- t =time in years
- wt = weighted average of cash flow at time t
- CFt = Cash flow at time t
Where:
| wt = | CFt / (1 + ytm)t Bond Price | = | Present Value of Cash Flow Bond Price |
- t =time in years
- wt = weighted average of cash flow at time t
- CFt = Cash flow at time t
- ytm = yield to maturity
| Modified Duration | = | DMac 1 + ytm/k |
- DMac = Macaulay Duration
- k = number of annual payments
| Effective Duration | = | − | ΔP/P Δi |
- Δi = interest rate differential
- ΔP = Bond price at i + Δi − bond price at i − Δi.
The formula for the duration of a coupon bond:
| Coupon Bond Duration | = | 1 + ytm ytm | − | (1 + ytm) + T (c − ytm) c [(1 + ytm)T− 1] + ytm |
- ytm = yield to maturity
- c = coupon interest rate in decimal form
- T = years till maturity
If the coupon bond is selling for par value, then the above formula can be simplified:
| Duration for Coupon Bond Selling for Face Value | = | 1 + ytm ytm | [ | 1 − | 1 (1 + ytm)T | ] |
- ytm = yield to maturity
- T = years till maturity
| Fixed Annuity Duration | = | 1 + ytm ytm | − | T (1 + ytm)T − 1 |
| Perpetuity Duration | = | 1 + y y |
- Δi = interest rate differential
- ΔP = Bond price at i + Δi −
bond price at i − Δi.
Portfolio Duration = w1D1 + w2D2 + … + wKDK
- wi = market value of bond i / market value of portfolio
- Di = duration of bond i
- K = number of bonds in portfolio
| Convexity | = | 1 P × (1 + ytm)2 | T ∑ t=1 | [ | CFt (1 + ytm)t | (t2 + t) | ] |
- P = bond price
- ytm = yield to maturity in decimal form
- T = Maturity in years
- CFt=Cash flow at time t
| ΔP P | = | −Dm | × | Δy | + | (Δy)2 2 | × | Convexity |
- Δy = yield change
- ΔP = Bond price change
Convexity can also be estimated with a simpler formula, like the approximation formula for duration:
| Convexity | = | P+ + P- − 2P0 2 × P0(Δy)2 |
- P0 = Bond price
- P- = Bond price when interest rate is incremented
- P+ = Bond price when interest rate is decremented
- Δy = change in interest rate in decimal form
Note, however, that this convexity approximation formula must be used with this convexity adjustment formula, then added to the duration adjustment:
| Convexity Adjustment | = | Convexity | × | 100 | × | (Δy)2 |
Hence:
| Bond Price Change | = | Duration | × | Yield Change | + | Convexity Adjustment |
Important Note! The convexity can actually have several values depending on the convexity adjustment formula used. Many online calculators calculate convexity with this formula:
| Convexity | = | P+ + P- − 2P0 P0(Δy)2 |
- P0 = bond price
- P- = bond price when interest rate is incremented
- P+ = bond price when interest rate is decremented
- Δy = change in interest rate in decimal form
Note that this formula yields double the convexity as the Convexity Approximation Formula #1. However, if this equation is used, then the convexity adjustment formula becomes:
| Convexity Adjustment | = | Convexity/2 | × | 100 | × | (Δy)2 |
- Δy = change in interest rate in decimal form.
As you can see in the Convexity Adjustment Formula #2 that the convexity is divided by 2, so using the Formula #2's together yields the same result as using the Formula #1's together.
To add further to the confusion, sometimes both convexity measure formulas are calculated by multiplying the denominator by 100, in which case, the corresponding convexity adjustment formulas are multiplied by 10,000 instead of just 100! Just keep in mind that convexity values as calculated by various online calculators can yield results that differ by a factor of 100. They can all be correct if the correct convexity adjustment formula is used!
The price value of a basis point (PVBP), or the dollar value of a 01 (DV01).
PVBP = |initial price − price if yield changes by 1 basis point|
(Math note: the expression |×| denotes the absolute value of ×.)