The Present Value and Future Value of Money
Money makes money. And the money that money makes makes more money.
— Benjamin Franklin
Money has a time value because it can be invested to make more money. Thus, a dollar received later has lesser value than a dollar received today. Conversely, a dollar received today is more valuable than a dollar received later because it can be invested to make more money. Formulas for the present value and future value of money quantify this time value, so that different investments can be compared. If a saver deposits $100 in a savings account today, and it pays 5% interest, what will it be worth 5 years from now, or 10 years from now? If an investor buys stock for $25, then sells it 3 years later for $45, what was its rate of return? A business has money and many ways to spend or invest it. What is the best use of that money?
The present value and future value of money, and the related concepts of the present value and future value of an annuity, allow an individual or business to quantify and minimize its opportunity costs in using money. Opportunity cost, in terms of using money, is the benefit forfeited by using the money in a particular way. For instance, if I spend $100 instead of depositing it in a bank that pays 5% interest, I forego the interest that I would have earned in the savings account by spending it instead of saving it, and if I would have saved it, then I forfeit the benefit of what I purchased. Of course, it might be possible to buy some stock, instead, that may double or triple, showing that the opportunity cost was even greater than originally thought. However, the future value of a stock is unpredictable, and the true opportunity cost of anything is really not knowable. However, the opportunity cost can be compared among specific investments where the rate of return depends on an interest rate that is either known or can be reasonable estimated by using the formulas for the present value and future value of money. Or a reasonable interest rate can be assumed simply to compare different investments.
The Future Value of a Dollar
The future value (FV) of a dollar is considered first because the formula is simpler.
The future value of a dollar is simply what the dollar, or any amount of money, will be worth if it earns interest for a specific time.
If $100 is deposited in a savings account that pays 5% interest annually, with interest paid at year-end, then after the 1st year, $5 of interest will be added to the $100 of principal for a total of $105. In the 2nd year, interest will be earned not only on the principal of $100, but also on the $5 of interest earned. Thus, at the end of the 2nd year, there will be 5 more dollars of interest earned from the principal added to the account, + 25¢ earned from the previous year's interest of $5. Thus, at the end of the 2nd year there will be $105 + $5 + $.25 = $110.25 total in the account. This is an example of compounding interest, interest that is paid on interest previously earned. This process can be continued for any number of years.
Expressing this as an equation, if P = principal and r = interest rate per year, then the amount of money in the account after the 1st year can be expressed by the equation P (1 + r) = P + r*P = $100 + .05 × 100 = $100 + $5 = $105. To find the amount after the 2nd year multiply 105 by the same factor — (1 + r). This equation can be expressed in terms of the 1st equation: P (1 + r) (1 + r), which reduces to P (1 + r)2. This equation can be extended to P (1 + r)n, with the superscript n equal to the number of years. Thus, the amount of money in the account after 3 years is P (1 + r)3. For this example, 100 (1 + .05)3 = 100 (1.05)3 = 100 × 1.157625 = $115.76, rounded to 2 decimal places.
| FV | = | PV × (1 + r)n |
- FV = Future Value of a dollar
- PV = Principal or Present Value
- r = interest rate per time period
- n = number of time periods
Using a calculator to determine future value:
If you have a calculator that has the exponential function — usually designated by the yx key — then this equation is easy to solve. Add the interest rate in decimal form to 1, then press yx, then enter 3, then press the = key. Take this product, the interest factor, and multiply it by the principal. So for our example, enter 1.05, then press yx, then enter 3, then press = to arrive at the interest factor 1.157625. Multiply this by 100 to get $115.76, the amount of money in the account after 3 years. Because exponentiation has priority over multiplication, you can also enter it this way: 100 X 1.05 yx 3 = $115.76.
Compounding Interest
In all formulas that compute either the present value or future value of money or annuities, there is an interest rate that is compounded at certain intervals of time. This interval is assumed to be 1 year, but, if it is less, as it frequently is, then 2 adjustments must be made to the formulas:
- The number of time periods must be changed to represent the number of times that interest is compounded. The number of years must be multiplied by the number of compounding periods within a year.
- The interest rate itself must be changed to reflect the interest rate per time period. The annual interest rate must be divided by the number of compoundings in a year.
Note also that most solutions to these formulas are rounded.
Example 1: Adjusting a Formula for Non-annual Compounding of Interest
If you put $100 in a savings account that pays 5% interest annually, but is compounded daily, how much will be in the account after 10 years?
Solution: This is finding the future value of a savings account, but since this account is compounded daily, the formula must be adjusted by dividing the interest rate by the number of periods and multiplying the exponent by the same number, as follows:
- c = number of compounding periods per year
Thus, we find the solution by plugging the values into the formula:
| FV | = | 100 × (1 + | .05 365 | )(10*365) |
| ≈ | 164.8665 | ≈ | $164.87 |
Note that with compounding interest, doubling either the interest rate or the amount of time more than doubles the amount of interest earned. For instance, $100 earning 5% interest that is paid yearly would equal $62.89 of earned interest after 10 years; after 20 years, earned interest would equal $165.33.
Thus, the future value of a dollar is the value that it will have after a specific time earning a specific interest rate.
The Present Value of a Dollar
Suppose you buy a zero coupon bond that matures in 10 years, then pays $1,000. How much is that future payment of $1,000 worth today at a 5% interest rate? In other words, if the prevailing interest rate is 5%, how much should you pay for a zero coupon bond that is sold at a discount to its par value?
In determining the future value of money, we know how much money we are starting with, and we want to know how much it will be worth later at a specific interest rate. When we know how much a future payment will be, then we want to determine what its value is today at a given interest rate.
The present value (PV) is the current value of a payment that will be received later. Discounting is the process of determining the present value of a payment from a known future payment, or future value. This is the reverse of determining the future value of a payment, because in this case, we already know the future value. It is found by dividing the future value by the same interest factor, (1 + r)n, used to determine future value. Since FV = PV × (1+r)n, then, dividing both sides by (1+r)n yields:
| PV | = | FV (1 + r)n |
Example 2: Calculating the Worth of a Zero Coupon Bond
How much would a zero coupon bond sell today, that pays $1,000 in 10 years, assuming an interest rate of 5% that is compounded and paid annually?
Solution: The zero coupon bond pays $1,000 in 10 years, so that is its future value in 10 years. If the prevailing interest rate is 5%, then to find the present value of the zero:
| PV | = | 1,000 (1 +.05)10 | = $613.91 |
Using a calculator to determine present value:
Enter 1,000, press the divide key, ÷ enter 1.05, then press the exponential key, yx, then enter 10, then the = key. The calculator should do the exponentiation 1st, because exponentiation has priority over division, then the division to arrive at the correct answer of $613.91, rounded to 2 places.
Summary: 1,000 ÷ 1.05 yx 10 = $613.91.
PV and FV Using Continuously Compounded Interest Rates
The formulas for present value and future value can be modified to calculate PV and FV for continuously compounded interest rates. We note that as n increases to infinity, this formula reaches a finite limit:
| As n → ∞, | ( | 1 | + | 1 n | ) | n | → e | = | 2.718281828... |
Consequently:
| As n → ∞, | ( | 1 | + | r n | ) | n | → er |
- r = interest rate per time period
- n = number of compounding periods
Therefore, these PV and FV formulas calculate the respective values using continuously compounded rates:
| FV | = | PV | × | ern |
| PV | = | FV | × | e−rn | = | FV ern |
Example 3: Calculating the FV for a Continuously Compounded Interest Rate
Sounds like you would make a fortune earning a continuously compounded rate, but not really. To show the small difference between a rate compounded daily and one that is compounded continuously, we calculate Example 1 using the continuously compounded rate: $100 in a savings account earning 5% interest annually, but is compounded continuously, will yield this FV after 10 years?
| FV | = | PV × ern |
| = | $100 × e(.05 × 10) | |
| = | $100 × e.5 | |
| ≈ | $100 × 1.648721 | |
| ≈ | $164.87 |
- FV = Future Value of Savings Account
- PV = Present Value
- r = interest rate per year
- n = number of years
- c = number of compounding periods in a year
If you use Microsoft Excel or the free OpenOffice Calc, the above is calculated thus: =100*EXP(0.5). Note that when rounded to the nearest penny, the continuously compounded rate equals the daily compounded rate:
| FV | = | 100 × | (1 + | .05 365 | )(10*365) |
| ≈ | 164.8665 | ≈ | $164.87 |
Calculating the Interest Rate of a Discounted Financial Instrument
To find the present value, we need to know the future value and the interest rate; to find the future value, we need to know the present value and the interest rate. But sometimes, both the present value and the future value are known, but not the interest rate. A good example of this problem is the zero coupon bond. A zero coupon bond pays no interest during its term, but is bought at a discount to its par value. Thus, in this case, the purchase price is known, which is its present value, and its future value is the par value of the bond, usually $1,000, paid when the bond matures. But what is the equivalent interest rate? As we will see below, even though a zero pays no interest, it still has an equivalent interest rate, which can be calculated and compared to other investments. (But, unfortunately, unless the zero is in a tax-deferred retirement account, you still have to pay taxes on the interest every year, even though you don't receive it until the zero matures!) How would it compare to a savings account that pays 5% interest compounded annually, for instance?
To find the equivalent interest rate, r, we transpose the equation for the future value of money to equal r. The equation for future value is:
Present Value × (1 + r)n = Future Value
First, divide both sides by the Present Value:
(1 + r)n = Future Payment/Present Value
Take the nth root of both sides:
1 + r = (Future Payment/Present Value)1/n
Then subtract 1 from both sides, to arrive at r, the interest rate for the discount:
| r = | ( | FV PV | ) | 1/n | − 1 |
| or | 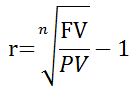 | ||||
- PV = Present Value
- FV = Future Value
- r = Interest Rate of Discount per time period
- n = number of time periods
Example 4: Calculating the Interest Rate of a Zero Coupon Bond
What interest rate is a zero coupon bond paying, that costs $600 and pays $1,000 in 10 years, assuming an interest rate that compounds annually?
Solution:
- Future Value = $1,000 par value
- Present Value = $600 purchase price
- n = 10 years
(1,000/600)1/10 − 1 = 5.24%
Using a scientific calculator: 1000 ÷ 600 = x√y 10 - 1 = .0524 = 5.24%
Note that if the interest is compounded at different intervals, such as quarterly or daily, then the interest rate r and the number of compounding periods must be adjusted. But if compounding of interest is not specified, as with the zero coupon bond, what value do we use? Use the value allowing a comparison with other investments. The interest rate can be compounded daily instead of annually, which will lower the interest rate. We would do this to compare the zero, for instance, to a savings account paying interest compounded daily. So how would our zero coupon bond example compare with a savings account paying 5%, compounded daily? In other words, if we put $600 in the savings account instead of buying the bond, would we have more or less than $1,000 after 10 years?
We can solve this problem in 2 ways. We can solve the problem either by calculating the future value of $600 earning 5% compounded daily, or we can calculate the equivalent interest rate for the zero coupon bond when compounded daily. In either case, we need to know how many compounding periods there are. With 365 days to a year, 10 years has 3,650 compounding periods. However, because the interest rate is listed as 5% annually, compounded daily, we need to find that .05/365 = .000136986 = the daily interest rate. Substituting these values into the IRD formula, the future value of the savings account is:
Future Value = 600 × (1 + .000136986)3650 = $989.20
We can already see that the zero coupon bond pays better, but let's see what the interest rate of the bond would be if compounded daily, like the savings account.
(1,000/600)1/3650 − 1
- = .000139962 (daily interest rate) × 365
- = .0511 = 5.11% annual interest rate.
Here we can see that, even though a zero and a fluorescent bulb pay no actual interest, we can find an equivalent interest rate that's compounded daily, weekly, quarterly, or whatever, so we can compare it to investments that do pay interest. This is the value of the formulas for the present value and the future value of money!
Interest Rate Conversions
In investments, pricing and returns are often expressed in interest rates compounded in specific time intervals. The interest rate or yield depends on the compounding period.
To find a compounded interest rate where the compounding period is shorter in duration that a given interest rate per period, simply take the appropriate nth root of 1 + the given interest rate, where n equals the number of compounding periods within the old time frame:
New Interest Rate = (1 + Old Interest Rate)1/n
For instance, if a bank account pays a nominal interest of 6% annually, then the equivalent interest rate compounded every 6 months would equal the square root of 1.06%, or 1.02956%. If the new compounding period is longer than the one given, then:
New Interest Rate = (1 + Old Interest Rate)n
where n = the number of compounding periods in the new period.
Thus, if a bank account paid 1.02956% interest semiannually, then that would be the equivalent of 6% per annum since (1.02956%)2 = 6%.
In many financial calculations, continuous compounding is used, especially in pricing derivatives. Converting continuous rates to discrete rates, and vice versa, is slightly more complicated. If c is a continuously compounded rate and rn is an equivalent rate that is compounded n times annually, then this equations must be true:
| PV | × | ec | = | PV | × | (1 | + | rn n | )n |
Divide both sides of the equation by PV:
| ec | = | (1 | + | rn n | )n |
Take the natural logarithm (ln) of both sides to find the continuous rate that equals the discrete rate compounded n times:
| c | = | n | × | ln (1 | + | rn n | ) |
- c = continuously compounded rate
- r = discrete interest rate
- n = number of compounding periods at rate r
The formula for finding the discrete rate compounded n times that equals a given continuously compounded rate:
| rn | = | n | × | (ec/n − 1) |
Math note: ln designates the natural logarithm of a number, such that if x = ey, then y = ln x.
Example 6: Converting a Discrete Rate into a Continuously Compounded Rate
If a bank account paid 5% annually, with biannual compounding, then the equivalent continuously compounded rate would be:
| r = 2 × ln (1 + | 5% 2 | ) = 4.9385% |
Example 7: Converting a Continuously Compounded Rate to a Discrete Rate
If a bank account pays a continuously compounded rate of 6% annually, but that is paid quarterly, then the equivalent rate compounded quarterly would be:
Quarterly Compounded Rate = 4 × (e(6%/4) − 1) = 6.0452%
The Calculation of Present Value and Future Value Assumes a Constant Monetary Unit of Measurement
Finally, something important to note. A tacit assumption is used to calculate a present value or future value: the monetary unit of measurement remains constant over the time period considered, meaning that the value of the unit of currency is the same at the beginning of the time period as it is at the end of that period. Though the value of money usually declines due to inflation, inflation is kept low and predictable by the central bank. However, if the government prints money irresponsibly, then the value of that money at some future date cannot be known, so the present value or the future value cannot be reliably calculated. Likewise, for types of money where the money cannot easily be created or destroyed, which will cause these types of money to fluctuate wildly in price over short time intervals. The value of money itself depends on the supply and demand of the money, just as for anything else. The value of most modern currencies is kept stable by central banks who vary the money supply according to the demands for money.
Gold and bitcoins are 2 prominent examples of money where the creation or destruction cannot easily be controlled, causing the value of individual units of money to vary widely in price. When the value of money itself fluctuates unpredictably, then present value or future value have no meaning since the price of the money itself will be unknown. So, if I deposit 100 bitcoins in a savings account, earning 5% interest annually, then I will have 105 bitcoins at the year-end, but I will have no idea what the value of those 105 bitcoins will be since the bitcoin itself may greatly differ in value 1 year from now.
And if the future value is unknowable, then a present value cannot be calculated from a future value, either. Because present value and future value are so important in assessing the value of investments and in making many business decisions, it is unlikely that a fluctuating currency like gold or bitcoins will ever be a major currency. Instead, these assets are purchased for speculation. It is, indeed, speculation since their future value is not ascertainable!
Conclusion
The present value and future value of a dollar is a lump sum payment. A series of equal lump sum payments over equal periods of time is called an annuity. This is a more general concept than the insurance product that most people think of when they see the word annuity; it includes loans, interest payments from bonds — even the annuity insurance product. Like the present value and future value of a dollar, the present value and future value of an annuity allows you compare investments, or the costs of loans. For instance, you can answer questions such as, How much would my payments be on a $200,000 mortgage with a 6% interest rate? or How much of a mortgage could I get, if the interest rate is 5%, but I can only afford to pay $1,000 per month? next: The Present Value and Future Value of an Annuity